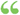 The areas of two triangles which have an angle of the one equal to an angle of the other are to each other as the products of the sides including the equal angles. A D A' Hyp. In triangles ABC and A'B'C', To prove AABC A A'B'C' A'B' x A'C ' Proof. Draw...  Elements of Plane Geometry: For the Use of Schools - Page 71by Nicholas Tillinghast - 1844 - 96 pagesFull view - About this book
 | 1902 - 482 pages
...triangles of the same altitude are to one another as their bases. 5. Equal parallelograms which nave an angle of the one equal to an angle of the other, have their sides about those angles reciprocally proportional. 6. Describe a rectilineal figure which... | |
 | 1903 - 898 pages
...inclined to Oil. Show that PQ is always parallel to a fixed straight line. 6. If two triangles have one angle of the one equal to an angle of the other, and the sides about those equal angles proportional, show that the triangles are similar. 7. A HC is an isosceles triangle... | |
 | University of St. Andrews - 1903 - 762 pages
...three consecutive rays are given. 4. Define reciprocally proportional, and prove thai parallelograms which have an angle of the one equal to an angle of the other and their sides about the equal angles reciprocally proportional are equal in area. TP and TQ are tangents... | |
 | James McMahon - Geometry, Plane - 1903 - 382 pages
...[Show that the triangles are halves of mutually equiangular parallelograms. ] Ex. If two triangles have an angle of the one equal to an angle of the other, and if the including sides are respectively as 1 : 3 and 1 : 4, show that the first triangle is one twelfth... | |
 | James McMahon - Geometry, Plane - 1903 - 380 pages
...proved that B"C" = B'C'. Two sides and included angle. 44. THEOREM 10. // two triangles have an angle of one equal to an angle of the other, and the sides about these angles proportional, then the triangles are similar. Let the triangles ABC and A'B'C' have the... | |
 | George Albert Wentworth - Geometry - 1904 - 496 pages
...other vertices of the polygon. D 190 AREAS OF POLYGONS. PROPOSITION VII. THEOREM. 410. The areas of two triangles which have an angle of the one equal to an angle of the other are to each other as the products of the sides including the equal angles. Let the triangles ABC and... | |
 | Education - 1879 - 944 pages
...they have two angles of the one equal to two angles of the other; Two triangles are similar If they have an angle of the one equal to an angle of the other and the including sides proportional ; Two triangles are similar If they have their sides respectively proportional."... | |
 | Cora Lenore Williams - Geometry - 1905 - 50 pages
...ratio of similitude. Prop. 110. Mutually equiangular triangles are similar. Prop. 111. If two triangles have an angle of the one equal to an angle of the other, and the including sides proportional, they are similar. Prop. 112. If two triangles have their corresponding... | |
 | Education - 1907 - 880 pages
...have two angles of the one equal to two angles of the other; Two triangles are similar if they have nn angle of the one equal to an angle of the other and the including sides proportional ; Two triangles are similar if they have their sides respectively proportional."... | |
 | Cora Lenore Williams - Geometry - 1905 - 122 pages
...parallelograms have two adjacent sides of the one equal respectively to two adjacent sides of the other, and an angle of the one equal to an angle of the other, the parallelograms are congruent. Prop. 78. Two rectangles are congruent if two adjacent sides of the... | |
| |
