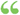 The areas of two triangles which have an angle of the one equal to an angle of the other are to each other as the products of the sides including the equal angles. A D A' Hyp. In triangles ABC and A'B'C', To prove AABC A A'B'C' A'B' x A'C ' Proof. Draw...  Elements of Plane Geometry: For the Use of Schools - Page 71by Nicholas Tillinghast - 1844 - 96 pagesFull view - About this book
 | Mathematics - 1835 - 684 pages
...interjacent side (c). 3. The three sides (/). 4. Two angles, and a side opposite to one of them . cor. 14 5. An angle of the one equal to an angle of the other, and the sides about two other angles, each to each, and the remaining angles of the same affection, or one of them a right... | |
 | Adrien Marie Legendre - Geometry - 1836 - 394 pages
...the general properties of triangles include, by implication, those of all figures. PROPOSITION XX. THEOREM. Two triangles, which have an angle of the one equal to an angle of the other, and the sides containing those angles proportional are similar, In the two triangles ABC, DEF, let the angles A and... | |
 | Benjamin Peirce - Spherical trigonometry - 1836 - 84 pages
...is the difference between DER and the surn of the other two triangles. 86. Lemma. If two triangles have an angle of the one equal to an angle of the other ; and the sides which include the angle in one triangle are supplements of those which include it in the other triangle... | |
 | Benjamin Peirce - Spherical trigonometry - 1836 - 92 pages
...8.) is the difference between DER and the sum of the other two triangles. 86. Lemma. If two triangles have an angle of the one equal to an angle of the other ; and the sides which include the angle in one triangle are supple- 1887) ments of those which include it in the other... | |
 | Benjamin Peirce - Geometry - 1837 - 216 pages
...equilateral or equiangular with respect to each other, are equivalent. 467. Lemma. If two triangles have an angle of the one equal to an angle of the other ; and the sides which include the angle in one triangle are supplements of those which include it in the other triangle... | |
 | Euclid, James Thomson - Geometry - 1837 - 410 pages
...parallelogram AB is equal to the parallelogram BC. Therefore equal parallelograms, &c. PROP. XV. THEOR. EQUAL triangles which have an angle of the one equal to an angle of the other, have their sides about those angles reciprocally proportional : and (2.) triangles which have an angle... | |
 | Adrien Marie Legendre - Geometry - 1838 - 382 pages
...the general properties of triangles include, by implication, those of all figures. PROPOSITION XX. THEOREM. Two triangles, which have an angle of the one equal to an angle of the oiher, and the sides containing those angles proportional, are similar. In the two triangles ABC, DEF,... | |
 | Euclides - 1840 - 192 pages
...an angle (BAD) of the other, have the sides about the equal angles reciprocally proportional : and, triangles which have an angle of the one equal to...of the other, and the sides about the equal angles reciprocally proportional, are equal. Let the triangles be so placed that the equal angles may be vertically... | |
 | Euclides - 1840 - 82 pages
...other, and the sides about the equal angles reciprocally proportional, are equal. PROP. XV. THEOR. Equal triangles which have an angle of the one equal to an angle of the other, have the sides about the equal angles reciprocally proportional : and triangles which have an angle... | |
 | Adrien Marie Legendre - Geometry - 1841 - 288 pages
...right-angled triangles. Thus the general properties of triangles involve those of all figures. THEOREM. 208. Two triangles, which have an angle of the one equal to an angle of the other, and the sides about these angles proportional, are similar. fig. 122. Demonstration. Let the angle A = D (fig. 122), and... | |
| |
