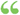 The areas of two triangles which have an angle of the one equal to an angle of the other are to each other as the products of the sides including the equal angles. A D A' Hyp. In triangles ABC and A'B'C', To prove AABC A A'B'C' A'B' x A'C ' Proof. Draw...  Elements of Plane Geometry: For the Use of Schools - Page 71by Nicholas Tillinghast - 1844 - 96 pagesFull view - About this book
 | John Keill - Logarithms - 1723 - 444 pages
...to AE asGFis to FL. Now fince ABE, FGL, are two Triangles, having one Angle of the one equal to one Angle of the other, and the Sides about the equal Angles proportional; the Triangle ABE will be * equiangular * 6 of tin's. to the Triangle FGL; and fo alfo fimilar to it.... | |
 | Euclid - 1728 - 236 pages
...DEFINITIONS. [milar right-lined Figures, as ABC, DCE, are fuch chat have each Angle oí the one equal to each Angle of the other, and the Sides about the equal Angles proportional. в с" The Ang. В= DCE ; and AB : BC : : DC : CE. alfo the Ang. A = D ; and BA : AC : : CD : DE. and... | |
 | Euclid, John Keill - Geometry - 1733 - 444 pages
...AE as GF is to* FL. Now fmce ABE, FGL, are two Triangles, having one Angle of the one equal to One Angle of the other, and the Sides about the equal Angles proportional ; .the Triangle ABE will be * equiangular * doftbit. to the .Triangle FGL; and alfo fimilar to it,... | |
 | John Playfair - Euclid's Elements - 1806 - 320 pages
...Wherefore, if the sides, &c. QE *D. PROP. VI. THEOR. IF two triangles have one angle of one equal to one angle of the other, and the sides about the equal angles proportional, the triangles will be equiangular, and will have those angles equal which are opposite to the homologous... | |
 | Daniel Cresswell - Euclid's Elements - 1817 - 454 pages
...chord has to the aggregate of the two chords that are next to it. PROP. VI. (XVII.) If two trapeziums have an angle of the one equal to an angle of the other, and if, also, the sides of the two figures, about each of their angles, be proportionals, the remaining... | |
 | Adrien Marie Legendre - Geometry - 1819 - 574 pages
...general properties of triangles involve those of all figures, THEOREM. 208. Two triangles, whkh Iiave an angle of the one equal to an angle of the other and the sides about these angles proportional, are similar. Fig. 122. Demonstration. Let the angle A = D (Jig. 122), and... | |
 | Daniel Cresswell - Geometry - 1819 - 486 pages
...FAE, FH :HE::AF:AE; that is, FG is to GE in the given ratio. PROP. XVU. 23. THEOREM. If two trapeziums have an angle of the one equal to an angle of the other, and if, also, the sides of the two ^figures, about each of their angles, be proportionals, the remaining... | |
 | Peter Nicholson - Architecture - 1823 - 210 pages
...BC2 but, since AB is equal to the sum of the two lines AD, DB, therefore AB2 = AC2 THEOREM 63. 161. Two triangles, which have an angle of the one equal to an angle of the other, are to each other as the rectangle of the sides about the equal Suppose* the two triangles joined,... | |
 | Adrien Marie Legendre - Geometry - 1825 - 280 pages
...the sides FG, GH, so that AB:FG::BC: GH. It follows from this, that the triangles ABC, FGH, having an angle of the one equal to an angle of the other...sides about the equal angles proportional, are similar (208), consequently the angle BCA = GHF. These equal angles being subtracted from the equal angles... | |
 | Adrien Marie Legendre, John Farrar - Geometry - 1825 - 280 pages
...right-angled triangles. Thus the general properties of triangles involve those of all figures. THEOREM. 208. Two triangles, which have an angle of the one equal to an angle of the other and the sides about these angles proportional, are similar. Demonstration. Let the angle A = D (Jig. 122), and let Fig.... | |
| |
