 | Euclid, John Playfair - Circle-squaring - 1819 - 348 pages
...all the angles of the figure, together with four right angles, that is, the angles of the figure are equal to twice as many right angles as the figure has sides, wanting four. COR. 2. All the exterior angles of any rectilineal figure are tegether equal to four... | |
 | Charles Hutton - Mathematics - 1822 - 618 pages
...outward, or inward angles, as the figure IMS sides : therefore the sum of all the inward and outward angles, is equal to twice as many right angles as the figure has sides. But the sum of all the inward angles, with four right angles, is equal to twice as many right angles... | |
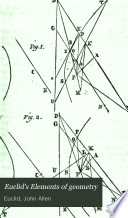 | Rev. John Allen - Astronomy - 1822 - 516 pages
...FC, FD, FE ; there are formed as many triangles as the figure has sides, all the angles of which are equal to twice as many right angles as the figure has sides [by this prop.] ; but of these all the angles about the point F are equal to four right angles [Ctor.... | |
 | Euclid - 1822 - 179 pages
...Cor. 6. All the internal angles of any rectilineal figure, ABCDE, together with four right angles, are equal to twice as many right angles as the figure has sides. Take any point F within the figure and draw the right lines FA, FB, FC, FD, and FE. There are formed... | |
 | Edward Riddle - Nautical astronomy - 1824 - 572 pages
...angles as the figure has sides. But all the interior angles, and four right angles, are also together equal to twice as many right angles as the figure has sides, (Theo. 25.) Hence the interior and the exterior angles of the figure are, together, equal to the interior... | |
 | Peter Nicholson - Mathematics - 1825 - 372 pages
...I). Cor. 1 . All the interior angles of any rectilínea] figure, together with four right angles, are equal to twice as many right angles as the figure has sides. For any rectilineal figure ABCDE can be divided into as many triangles as the figure has sides, by... | |
 | George Lees - 1826 - 266 pages
...all the angles of the figure, together with four right angles ; that is, the angles of the figure are equal to twice as many right angles, as the figure has sides wanting four. PROP. XIII. THEOREM. If two triangles, BAG, EOF, have two angles, BAG, ABC, and a side... | |
 | John Radford Young - Euclid's Elements - 1827 - 208 pages
...the single interior opposite angle CDE. PROPOSITION XVir. THEOREM. In any polygon the sum of all the angles is equal to twice as many right angles as the figure lias sides, all but four right angles. For if from the vertices of the several angles, lines be drawn... | |
 | Robert Simson - Trigonometry - 1827 - 513 pages
...zi. COR. 1. All the interior angles of any rectilineal figure, together with four right angles, are equal to twice as many right angles as the figure has sides. For any rectilineal figure ABCDE, can be divided into as many triangles as the figure has sides, by... | |
 | John Radford Young - Euclid's Elements - 1827 - 246 pages
...in each triangle amounts to two right angles, therefore the angles of all the triangles are together equal to twice as many right angles as the figure has sides, that is to say, the sum of the angles of the polygon, together with those about the point within it,... | |
| |
All the interior angles of any rectilineal figure, together with four right angles, are equal to twice as many right angles as the figure has sides. 
