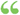 The areas of two triangles which have an angle of the one equal to an angle of the other are to each other as the products of the sides including the equal angles. D c A' D' Hyp. In triangles ABC and A'B'C', ZA = ZA'. To prove AABC = ABxAC. A A'B'C' A'B'xA'C'... The areas of two triangles which have an angle of the one equal to an angle of the other are to each other as the products of the sides including the equal angles. D c A' D' Hyp. In triangles ABC and A'B'C', ZA = ZA'. To prove AABC = ABxAC. A A'B'C' A'B'xA'C'...  Elements of Geometry: With, Practical Applications - Page 120by George Roberts Perkins - 1850 - 320 pagesFull view Elements of Geometry: With, Practical Applications - Page 120by George Roberts Perkins - 1850 - 320 pagesFull view - About this book
 | Daniel Cresswell - Euclid's Elements - 1817 - 454 pages
...chord has to the aggregate of the two chords that are next to it. PROP. VI. (XVII.) If two trapeziums have an angle of the one equal to an angle of the other, and if, also, the sides of the two figures, about each of their angles, be proportionals, the remaining... | |
 | Adrien Marie Legendre - Geometry - 1819 - 574 pages
...general properties of triangles involve those of all figures, THEOREM. 208. Two triangles, whkh Iiave an angle of the one equal to an angle of the other and the sides about these angles proportional, are similar. Fig. 122. Demonstration. Let the angle A = D (Jig. 122), and... | |
 | Daniel Cresswell - Geometry - 1819 - 486 pages
...FAE, FH :HE::AF:AE; that is, FG is to GE in the given ratio. PROP. XVU. 23. THEOREM. If two trapeziums have an angle of the one equal to an angle of the other, and if, also, the sides of the two ^figures, about each of their angles, be proportionals, the remaining... | |
 | Peter Nicholson - Architecture - 1823 - 210 pages
...equal to the sum of the two lines AD, DB, therefore AB2 = AC2 THEOREM 63. 161. Two triangles, which have an angle of the one equal to an angle of the other, are to each other as the rectangle of the sides about the equal Suppose* the two triangles joined,... | |
 | Adrien Marie Legendre - 1825 - 570 pages
...: FH : : CD : HI ; but we have seen that the angle ACD = FHI; consequently the triangles ACD, FHI, have an angle of the one equal to an angle of the other and the sides about the equal angles proportional ; they are therefore similar (208). We might proceed in the same manner... | |
 | Adrien Marie Legendre, John Farrar - Geometry - 1825 - 294 pages
...AC : FH : : CD : HI; but we have seen that the angle ACD = FHI; consequently the triangles ACD, FHI, have an angle of the one equal to an angle of the other and the sides about the equal angles proportional ; they are therefore similar (208). We might proceed in the same manner... | |
 | Adrien Marie Legendre, John Farrar - Geometry - 1825 - 280 pages
...the general properties of triangles involve those of all figures. THEOREM. 208. Two triangles, which have an angle of the one equal to an angle of the other and the sides about these angles proportional, are similar. Demonstration. Let the angle A = D (Jig. 122), and let Fig.... | |
 | Adrien Marie Legendre - Geometry - 1825 - 276 pages
...the sides FG, GH, so that AB:FG::BC: GH. It follows from this, that the triangles ABC, FGH, having an angle of the one equal to an angle of the other and the sides about the equal angles proportional, are similar (208), consequently the angle BCA = GHF. These equal angles... | |
 | Walter Henry Burton - Astronomy - 1828 - 84 pages
...F, are equal; and so, if 'the angles at F had been supposed equal, the triangles would have had each angle of the one equal to an angle of the other, and the side CF lying between correspondent angles in each; whence also DF is equal to FE. Is this sufficiently... | |
 | George Darley - Geometry - 1828 - 190 pages
...equal." Here we have a criterion whereby to judge of the equality of two triangular surfaces, which have an angle of the one equal to an angle of the other. For example : ABCD is a road cutting off a triangular field AOB. It is desirable that the line of road... | |
| |